Die Online-Seite Mathigon.org bietet unter anderem das Polypad an, eine interaktive Zeichenfläche, die auf Mathematik spezialisiert ist. Unter anderem gibt es eine interaktive Waage, die ich zur Einführung von Gleichungen und den Äquivalenzumformungen sinnvoll finde.
Warum nicht GeoGebra verwende? Naja, es gibt ja durchaus einige Zeichnungen, die ganz nett sind, aber sie sind, in der Erstellung recht umständlich. Mit dem Polypad auf Mathigon.org kann ich dagegen sofort anfangen, ohne Vorbereitung, aber auch vorbereitete Arbeitsblätter schnell nach Bedarf anpassen.
In diesem Artikel möchte ich zum einen Mathigon vorstellen, aber auch Unterrichtsmaterialien, die ich schon eingesetzt habe.
Schritt 1: Zahlenkacheln
Fängt man mit der Waage auf Mathigon an, probiert man vermutlich erst einmal die Zahlenkacheln und die sind, wie ich finde, als Einstieg durchaus geeignet.

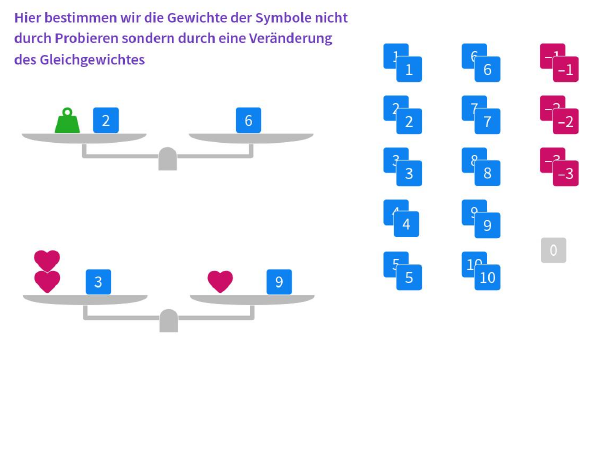
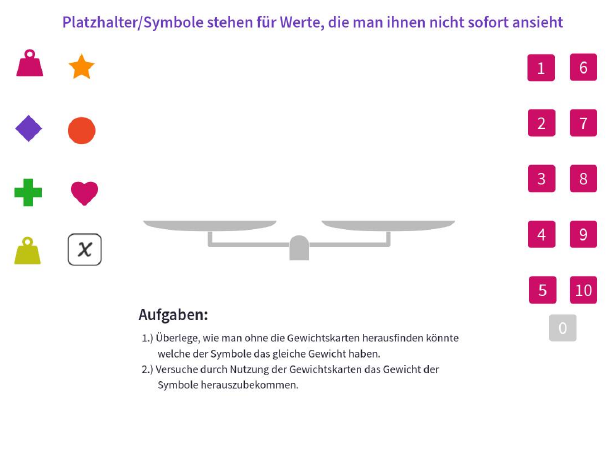
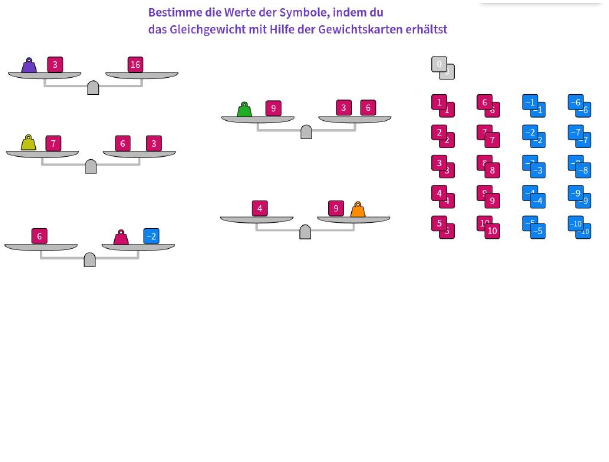
Diese vier Zeichnungen, die man einzeln aufrufen kann aber durchaus auch in HTML einbetten kann sind als Einführung in das Waagenmodell an sich gedacht. Ich habe als Zugang ein Arbeitsblatt mit QR-Codes erstellt, das ihr gerne nutzen könnt Download. In moodle könnte man das ganze natürlich einzeln verlinken, oder den Inhalt des PDFs als Textseite mit den Links anbieten. Auf jeden Fall gehört zu solch einer „Spielaufgabe“ immer ein Auftrag, damit es nicht nur durchgespielt wird. Die Aufgaben an sich können aber als Hausaufgaben gegeben werden, denn es ist nicht so schwierig.
Kleine Hintergrund-Info: die Zahlenkarten haben das Gewicht, das auf Ihnen steht. Ich habe die Farben abgeändert, weil mir jemand erzählt hat, dass „blau“ besser zu negativ (kalt = gefroren) und „rot“ besser zu positiv (warm) passt, also quasi angepasst auf Farben, die man bei Temperaturen verwendet.
Die Symbole, die da zu sehen sind, werden auch von Mathigon gestellt, aber letztendlich kann ich jedes Bild verwenden. Der Kasten mit dem x stammt auch von mir. Üblicherweise haben alle Symbole und Bilder eine Gewicht von „1“. Wenn ich es nicht ausgeschaltet habe, kann ich dem Symbol aber ein anderes, beliebiges Gewicht geben. Dazu klicke ich den Mittelteil der Waage an und wähle den Eintrag „Balance“ an. In meinen Arbeitsblättern/Zeichnungen ist dies nicht verfügbar, denn ich habe es deaktiviert. Es würde stören, wenn die Schüler damit experimentieren.
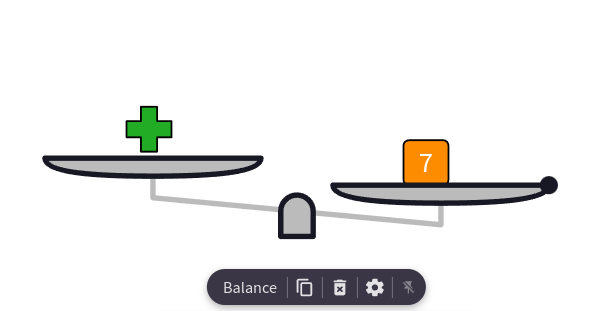
Klicke ich „Balance“ an, wird die Waage ausbalanciert und das grüne Kreuz bekommt damit das Gewicht bzw. den Wert 7. Und zwar alle diese grünen Kreuze auf dem Zeichenblatt, egal welches ich dem Wert 7 gebe. Und das ist auch sinnvoll, damit es nicht verwirrt und gleiche Symbole auch keine unterschiedlichen Werte haben. Gleiches Prinzip gilt für Bilder, wie das x im Kasten, dass ich einfügen kann. Brauche ich das „x“ mehrfach, dann kopiere es es einfach und habe wieder das gleiche Gewicht!
Von der Kachel zum weiterverwendbaren Modell
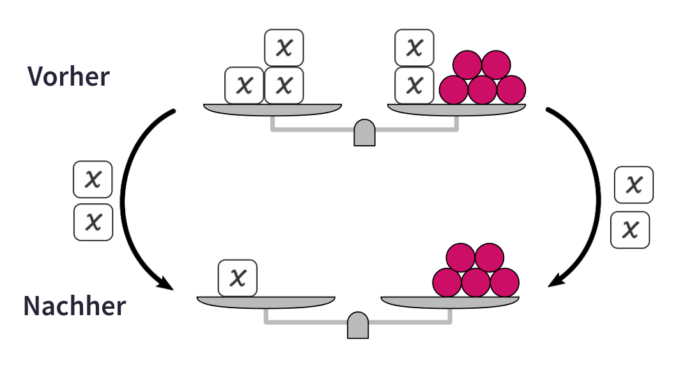
Dieses Modell mit den Zahlenkarten ist nicht so ganz praktisch, denn um etwas abzuziehen muss man die Zahlenkarten aufteilen und dann etwas wegnehmen oder aber Karten mit negativen Werten verwenden. Das ist schwer interpretierbar! Also gehen wir von den Zahlenkarten zu dem Modell über, dass üblicherweise in Schulbüchern verwendet wird. Mit negativen Zahlen in Gleichungen kann es immer noch nicht umgehen, aber es geht ja erst einmal um das Grundverständnis.
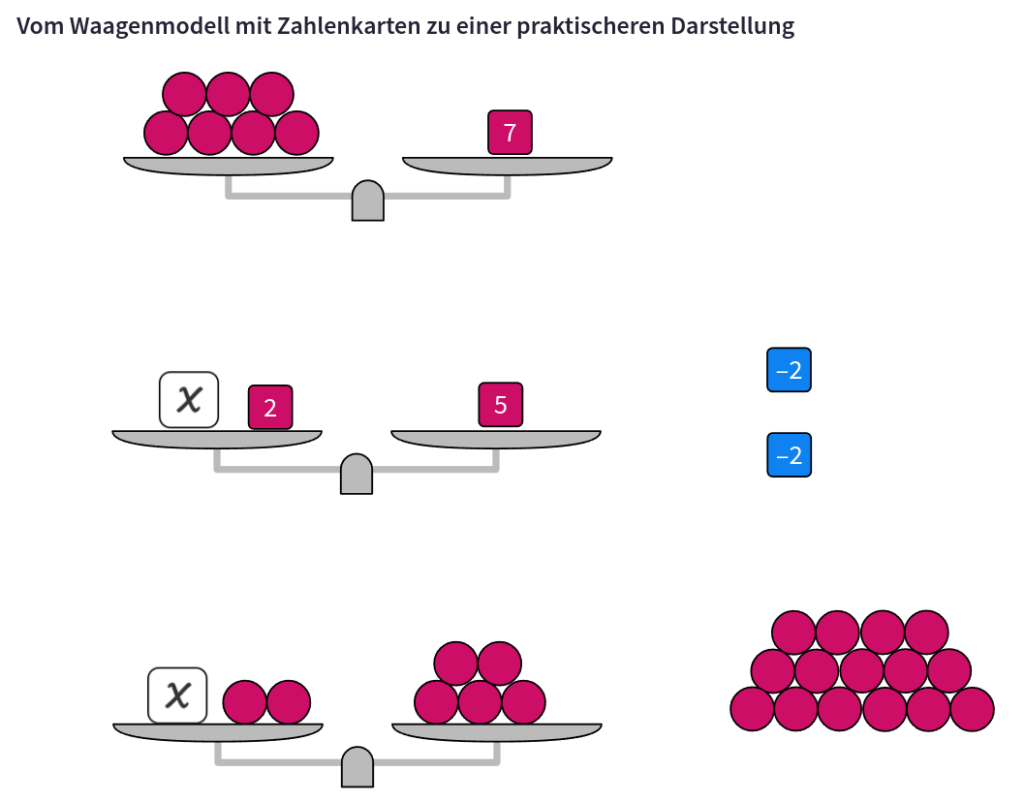
Diese Zeichnung ist hier erreichbar.
Der Umstieg scheint mir für die Schüler kein Problem zu sein. Als ich es Unterricht verwendet habe und die letzte Zeichnung „vergessen“ hatte (Hüstel), konnten die Schüler die folgenden Zeichnungen ohne Probleme nutzen.
Einführung des Begriffes Äquivalenzumformung
Mit dem Modell, wo ich statt Zahlkarten Kugeln verwende und in dem jede Kugel den Wert „1“ hat, kann ich mich nun konzentrieren auf die Äquivalenzumfromungen. Man könnte in den Schulbüchern sich anschauen, welche Erklärungen es zu dem Begriff gibt und die Schüler probieren dann wiederrum einige Zeichnungen aus. Letztendlich haben die Schüler in den ersten Beispielen schon unbewusst Äquivalenzumformungen durchgeführt. Klar, hier sind die Zahlenwerte so klein, dass man leicht im Kopf den Wert des Symboles bestimmen kann, aber es geht natürlich um das Prinzip, das muss man den Schülern klar machen, besonders wenn sie sich beschweren, dass es zu leicht ist.
Da wir in der viertletzten Woche vor den Sommerferien sind und die Noten gemacht sind, sind vielleicht einige Schüler nicht mehr so ganz dabei. Aber der spielerische Aspekt führt dazu, dass sie immerhin nicht was anderes machen sondern eher versuchen das Modell auszutricksen.
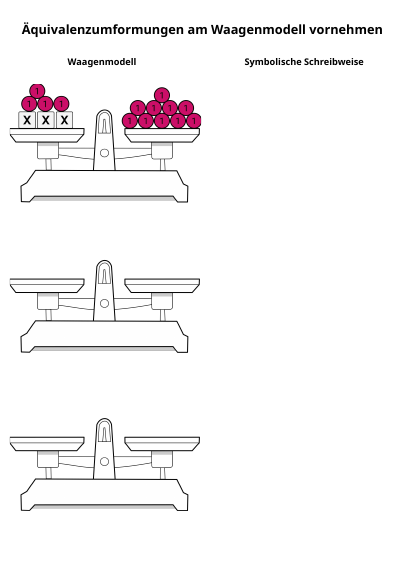
Für den Zugriff auf die Zeichnungen, um die die Äquivalenzumformungen kennenzulernen, habe ich wieder QR-Codes erstellt. Angedacht ist, dass man die erste Seite ein paar Mal ausdruckt, vielleicht auch laminiert und die Schüler dann den QR-Code mit einem Tablet scannen und dann die Zeichnung nutzen können.

Die zweite Seite ist als Erklärung für den Lehrer gedacht. Man kann das PDF (Download) auch online, zum Beispiel in moodle, nutzen, denn die Links sind anklickbar.
Jede Seite enthält eine vorbereitete Waage mit einem kleinen Auftrag. Beim Thema „Subtraktion“ könnte man zum Beispiel schön zeigen, dass man etwas wegnimmt, indem man es an die Pfeile (von mir eingefügte Bilder!) dranschiebt bzw. dranschreibt.
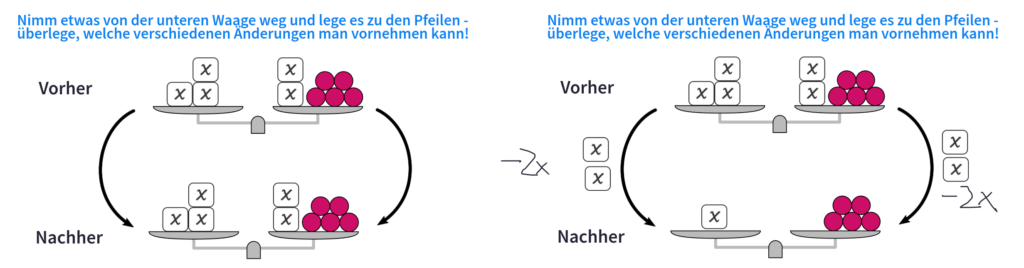
Das Beschreiben ist ein durchaus interessanter Aspekt, wie ich finde, denn ich kann also etwas in die Zeichnung reinmalen, ohne dass es das Gewicht stört. Eventuell muss ich noch einmal die Aufträge überdenken, denn einige sind nicht ganz so klar. So haben die Schüler bei der Addition einfach multipliziert. Man könnte das natürlich auch thematisieren, indem die Schüler bzw. jede Gruppe eine der Äquivalenzumformungen vorstellt. Und dann würden das sicher einige kritisieren.
Angedacht ist, dass wir diese Prinzipien dann vielleicht nutzen, um die Äquivalenzumformungen durchführen zu können, um die Gleichung zu lösen bzw. hier den Wert von „x“ zu bestimmen. Das könnte man dann in Mathigon zum Beispiel so auf“schreiben“.
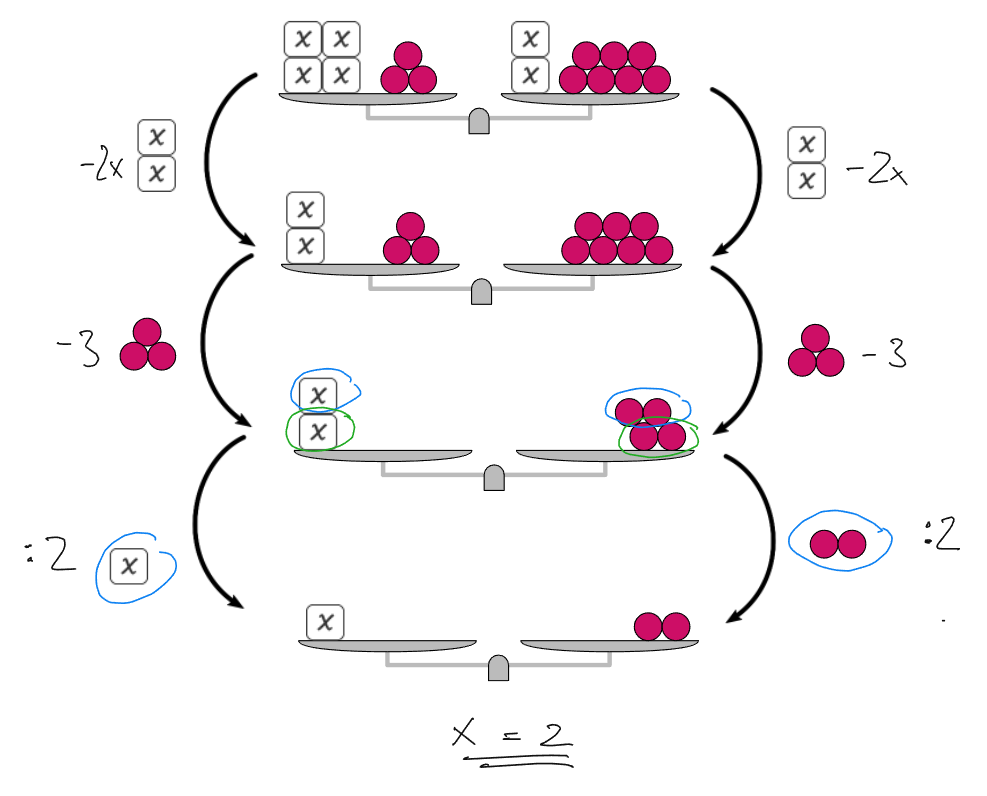
Einfach immer die vorherige Zeichnung kopieren und darunter einfügen (die Pfeile könnte ich schon vorbereiten) und dann jeweils das, was man wegnimmt, an die Pfeile verschieben. Nur bei „Geteilt“ ist es etwas schwieriger, aber daher habe ich die Hälften farbig eingekreist.
Äquivalenzumformungen am Waagenmodell üben
Nach der Einführung des Begriffes „Äquivalenzumformung“ würde ich die Schüler ein wenig üben lassen, wobei ich schon die mathematischen Formulierungen für die Umformungen verwende, wie es im letzten Bild zu sehen war. Ich habe dazu ein paar H5P-Quizze erstellt, es könnten aber noch mehr kommen.
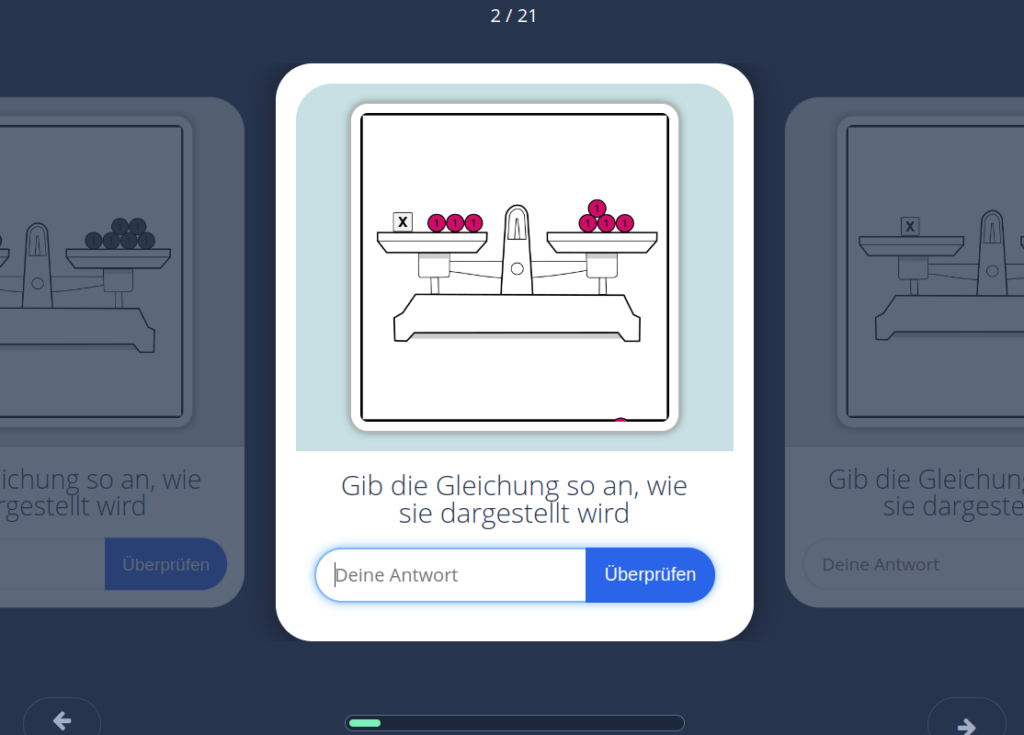
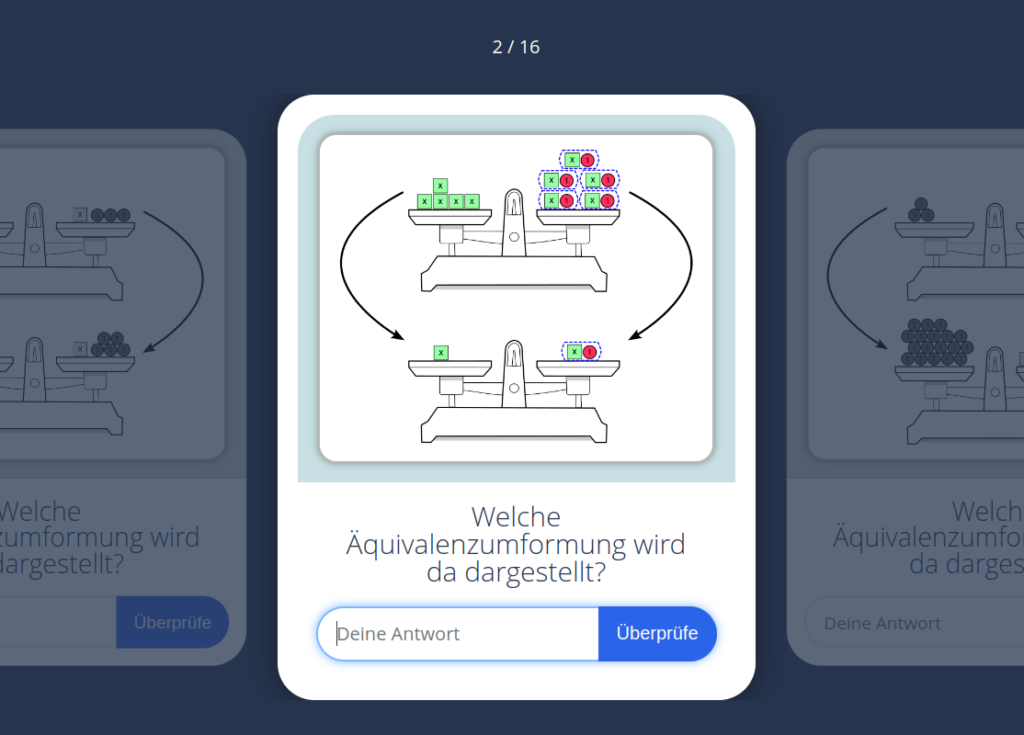
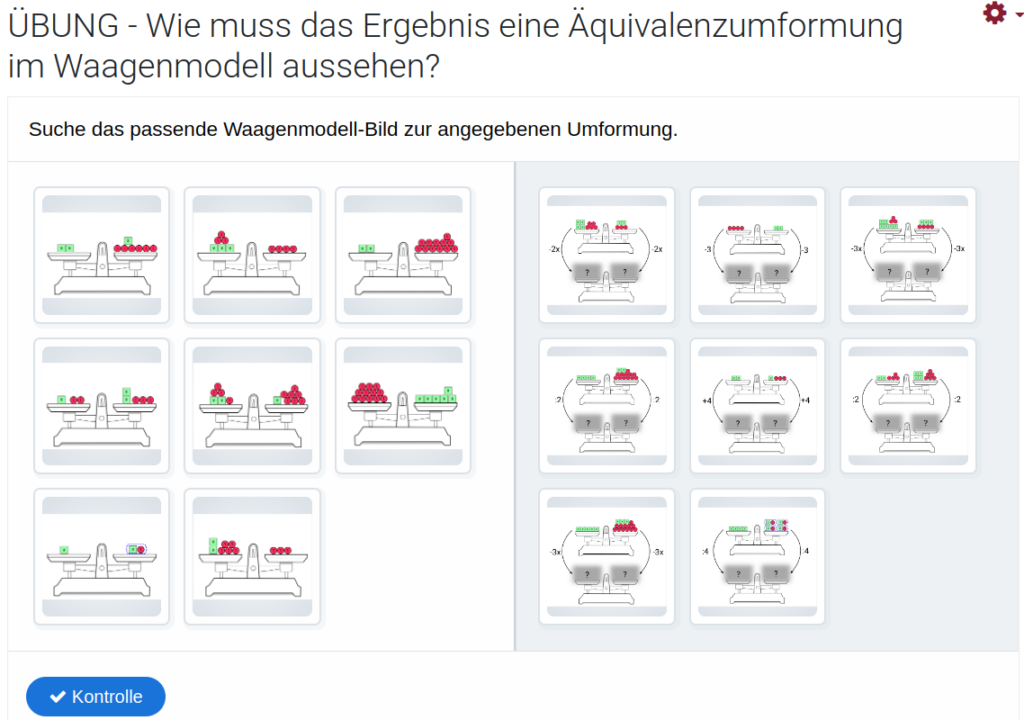
Die Schüler können das in moodle erledigen und ich sehe noch, ob und wie sie es gemacht haben. Die Quizze werde ich noch bei vielleicht apps.zum.de oder über die Campus-Cloud von RLP veröffentlichen, aber die vielen Bilder müssen bei der ZUM immer mit Quellenangaben versehen werden und das kostet so viel Zeit. Die Bilder habe ich übrigens selber in Inkscape erstellt und davon einfach ein Screenshot gemacht. Die Zeichnung ist hier verfügbar.
Die Aufgaben sind nicht so schwer, aber es geht hier wirklich nur darum, das Prinzip ein wenig zu üben und es zu festigen. Die schwierigeren Gleichungen und eine rein formale Bearbeitung von Gleichungen kommt dann noch.
Fazit
So richtig 100% hat noch nicht alles geklappt, zumal einige Zeichnungen nicht mehr bewegliche Waagen hatten, die also nicht auf die Gewichte reagiert haben. Inzwischen weiß ich, woher es kam, denn es liegt an der Einstellung „Undo und Redo“ die aktiviert sein muss. Verstehen tue ich es nicht, aber egal … hauptsache die Zeichnungen machen was sie soll. Ich werde das mal dem Entwickler melden.
An sich hat es aber gut funktioniert und ich bin soweit zufrieden. Auch wenn es technische Probleme gab (die Laptops am Laptop-Waagen waren nicht alle geladen 🙄) und eben das mit der Waage, war die letzte Stunde keine Katastrophe und es war sicher verständlich, um was es geht. Das hätte sicherlich eleganter ablaufen können, aber es war ja das erste Mal.
Daher ist mein Fazit doch positiv und so richtig stark wird das Waagenmodell sich auch erst auswirken, wenn wir zu schwierigeren Äquivalenzumformungen kommen.
In der nächsten Stunde führe ich die Anwendung der Äquivalenzumformungen ohne das Waagenmodell ein. Dazu übertragen wir eine Gleichung und die Äquivalenzumformungen von der Waage auf die formale Schreibweise (Arbeitsblatt dazu).
Und ich bereite die Waage auch in Mathigon vor, um die Äquivalenzumformungen nicht nur erinzuzeichnen, sondern es auch gleich durchzuführen. Weitere Beispiele dieser Art können dann folgen!
Antworten