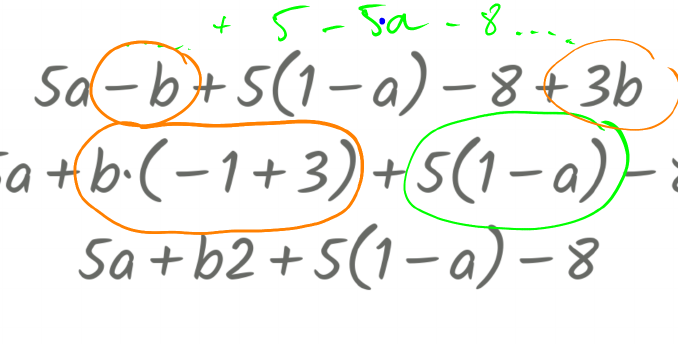
Viele Lehrer haben noch keine Idee, wie man GraspableMath nutzen kann und sehen nur „das übernimmt ja alles was die Schüler machen müssen“. Klar, man muss seine Stunden abändern, damit der Einsatz von GraspableMath wirklich sinnvoll ist. Nicht nur Termumformungen einfach ausführen, sondern eher ausprobieren und dabei lernen was möglich ist.
Hausaufgabe: Einführung in GraspableMath
Damit die Schüler GraspableMath bedienen können, ist es sinnvoll, sie ein paar einfache Übungen durchführen zu lassen. Ich habe dazu zwei Aktivitäten vorbereitet, also Sammlungen von kleinen Aufgaben, die auch auf ihren Abschluss kontrolliert werden können. Aufgrund des Zeitdruckes kam ich nur zur Vorbereitung zweiter Aktivitäten:
- GraspableMath kennenlernen – mit den wichtigsten Handgriffen und einem größeren Rechenterm
- Brüche in GraspableMath bearbeiten (Grundlagen 1) – Vor allem die Multiplikation von Brüchen und erweitern und Kürzen
(beide sind hier anonym nutzbar!)
Grundlagen 2 zu Brüchen habe ich (damals) vorher nicht mehr geschafft zu erstellen. Das wird nachgereicht.
Die Schüler sollten das die Woche über zu Hause erledigen. Leider musste ich bei einigen mehrfach nachfragen und eine Nacharbeitung am Nachmittag androhen, damit es erledigt wurde.
In der Lehrer-Ansicht mit den Ergebnissen und Schritten der Schüler sehe ich, wie sie bei der Lösung vorgegangen sind. Man konnte sehen, dass sie teilweise nicht die Anleitungen durchgelesen hatten. Dann hatte ich über Sdui oder in der Schule sie angesprochen und darauf hingewiesen, warum es bei Ihnen nicht ging. Teilweise konnte man auch erkennen, dass einige Schüler – gerade bei dem größeren Rechenterm in der Einführung – nicht gezielt die Vorrangsregeln erkannt haben, sondern fälschlicherweise Zahlen verschoben haben, wo es notwendig war. Auch bei denen habe ich mal nachgefragt, ob das klar ist.
Einführung in Variablen
Wir haben vorher die Addition und Subtraktion von rationalen Zahlen eingeführt und geübt. Ich hänge die Einführung in die Termumformung mit Variablen gleich an, da ich die Erfahrung gemacht habe, dass die Schüler bei den Umformungen die klassischen Fehler machen, die bei den rationalen Zahlen eingeführt werden. Mit der Einführung der Variablen-Terme gebe ich meiner Meinung nach den Rechen- und Vorrang-Regeln eine größere Bedeutung und hoffe, dass die Schüler erkennen, warum wir sie behandelt haben. Denn reine Zahlenterme könnten ja mit dem Taschenrechner bearbeitet werden.
Als Vorbereitung erinnerte ich die Schüler an die Bedeutung von Variablen (dies wurde bereits in Klasse 5 behandelt) und wo sie wichtig sind (z.B. Formeln für Berechnungen, allegemeine Aussagen zu Rechengesetzen, wichtig im Computer, etc.). Vor allem, dass sie Platzhalter für Zahlen sind. Wir haben ein paar Beispiele für Formeln mit Variablen gesucht und was Sie bedeuten.
Dann habe ich die Schüler darauf vorbereitet, dass wir in der nächsten Stunde GraspableMath nutzen werden, um Terme mit Variablen zu vereinfachen. Denn es ist bei großen Termen sinnvoll, sie so weit wie möglich zu „verkleinern“, damit man bei der Berechnung von Werten, wenn man für eine Variable also eine Zahl einsetzt, weniger und einfachere Rechnungen hat.
Entdecken der Möglichkeiten zu Termumformungen
Dann haben die Schüler eine Stunde lang (also 45 Minuten) an dieser Aktivität Umgang mit Variablen (1) (Lehrer-Ansicht) gearbeitet:
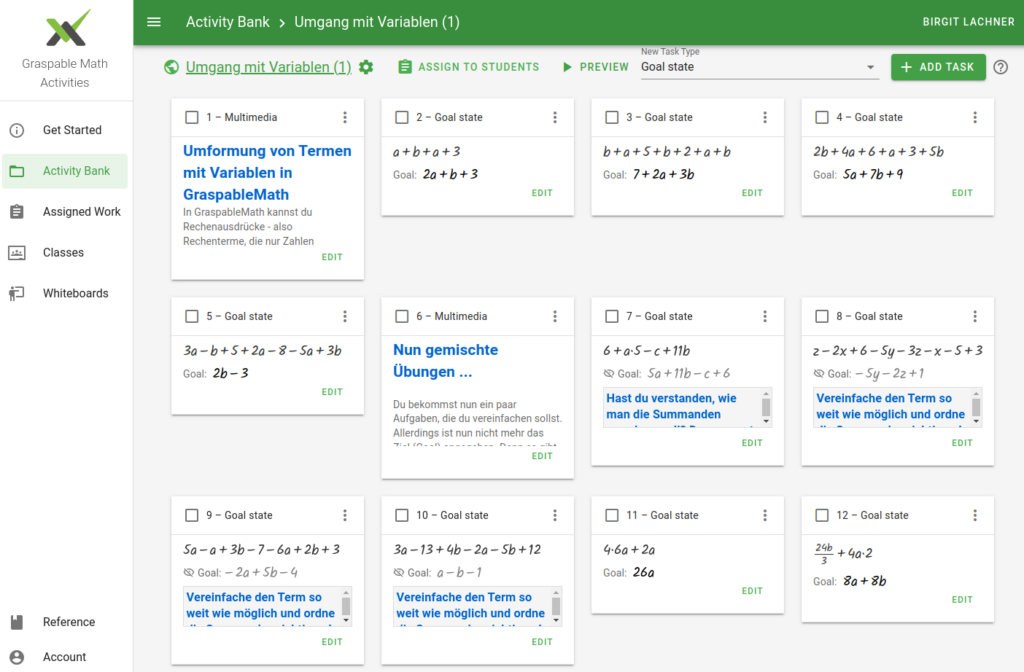
Sie sollten nicht nur die Aktivität bearbeiten und jeweils das vorgegeben Ziel erreichen, sondern sich gleichzeitig auf einem Arbeitsblatt Notizen machen. Dazu gehört das Aufschreiben der Umformung zu gestellten Aufgaben und sie sollten versuchen, eine allgemeine Regel zu notieren.
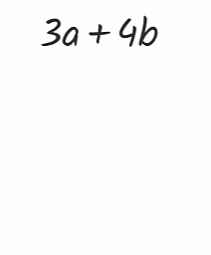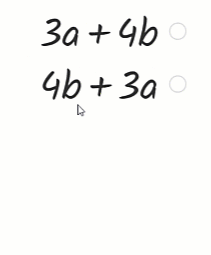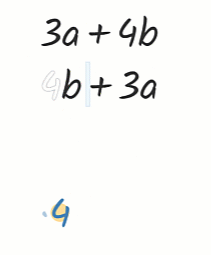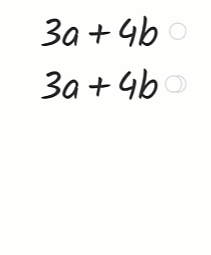
Wie zu erwarten waren einige Schüler schnell fertig mit den 13 Seiten/Aufgaben. Aber sie hatten sich nichts notiert und musste noch einmal von vorne anfangen.
Auf Seite der Bedienung von GraspableMath war ein Aspekt neu, den sich einige nicht gleich gemerkt haben. Beim Herumgehen habe ich das den Schülern noch einmal gezeigt. Es ging darum, dass man Summanden mit Zahlenfaktor und Variable nicht so einfach verschieben kann. Ein GIF und Begleittext hatte es eigentlich erklärt. Das GIF habe ich übrigens mit Camtasia aufgenommen.
Die einzelnen Aufgaben waren nicht immer einfach und irgendwann war ja auch das Ziel nicht mehr gegeben. Das hat dann dazu geführt, das der eine oder die andere schon mal ein lautes „JA!“ hören ließ, als die Aufgabe als abgeschlossen, also grün, angezeigt wurde.
Gefallen hat mir auch, das einige Schüler über die Regeln und Ergebnisse bei den Aufgaben diskutiert haben. Genau das ist es, was wir brauchen. Die Schüler müssen über Mathe reden und Ideen formulieren!
Hausaufgabe war, das Blatt weitgehend fertig auszufüllen.
Zusammentragen der Erfahrungen zu dem Umformungen
In der folgenden Stunde habe ich den Schülern zuerst gezeigt, was mir aufgefallen ist, als ich mir die Lösungsschritte für die Aufgabe mit den Begriffen angesehen habe. In der Lehreransicht zur Aktivität kann ich zumindest vom letzten Lösungsversuch sehen, wie sie vorgegangen sind und welche Schritte sie gemacht haben. Dazu habe ich in der Übersicht geschaut, wer eher mehr Schritte gebraucht hatte und meist ist der Grund dafür eine falsche Vorgehensweise.
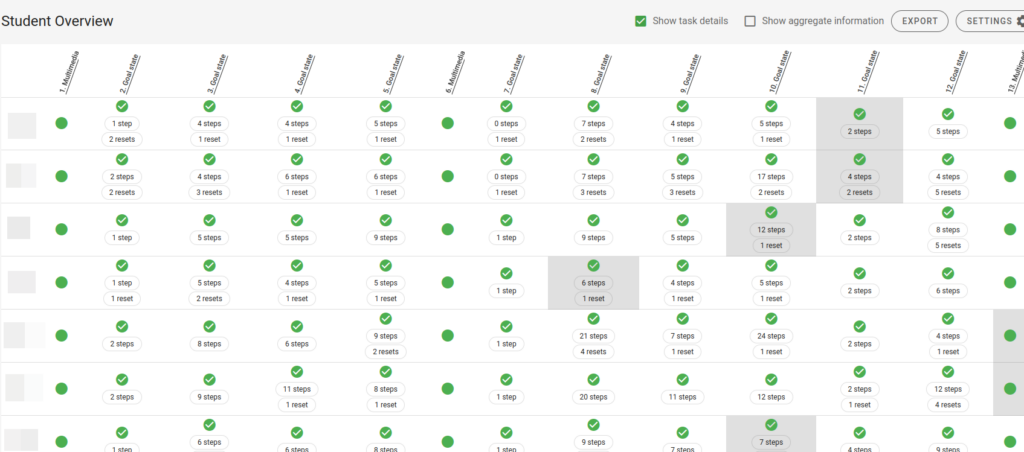
Von einigen Schritten habe ich Screenshots gemacht und für das Zeigen am Beamer zusammengefasst.
Ich habe die Schüler gefragt, ob sie erkennen können, ob es sich um einen Fehler aufgrund eines Fehlverständnisses handelt (man kann keine Summanden mit unterschiedlichen Variablen addieren) oder um eine falsche Bedienung (man zieht nicht am Vorzeichen des Summanden, sondern an der Zahl oder der Variablen).
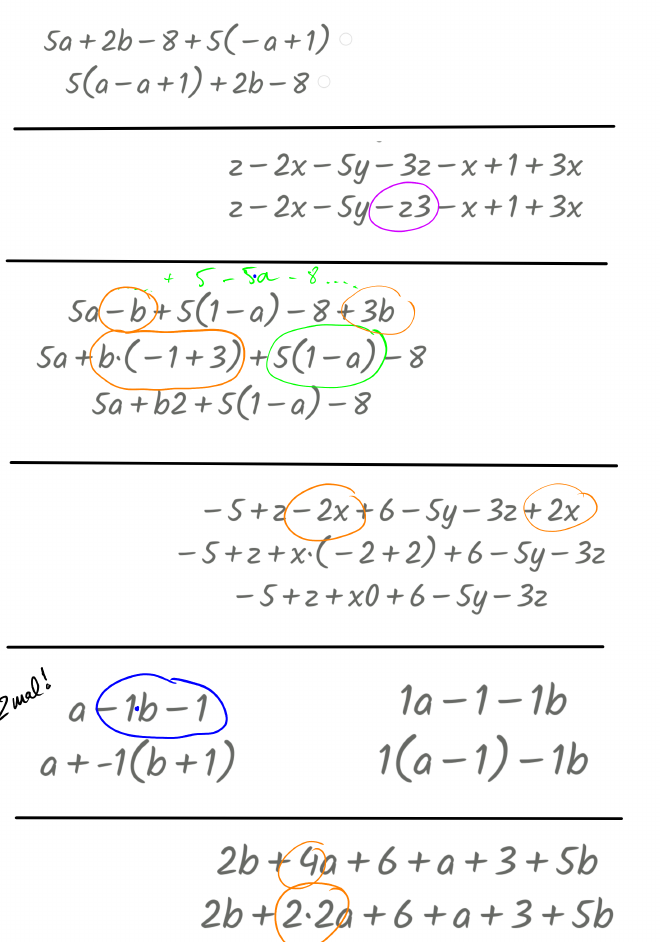
Mit ein Ziel war es, nicht nur an die Bedienung zu erinnern, sondern auch noch einmal erwähnen, dass ich nur Summanden addieren kann, die dieselben Variablen haben.
Und … bei der Nutzung von GraspableMath geht es nicht unbedingt darum, einfach das Ziel zu erreichen, sondern sich vorher zu überlegen, was man warum machen will/kann und sich vorher zu überlegen, was das Ergebnis sein müsste.
Nach dieser kurzen Anfangs-Phase haben wir die Tabelle gemeinsam im Gespräch ausgefüllt, die Schüler haben mir Vorschläge für Ergebnisse und für allgemeine Regeln gemacht. Zum Ende der Stunde fehlte noch etwas, was wir dann in der folgenden Stunde erledigt haben.
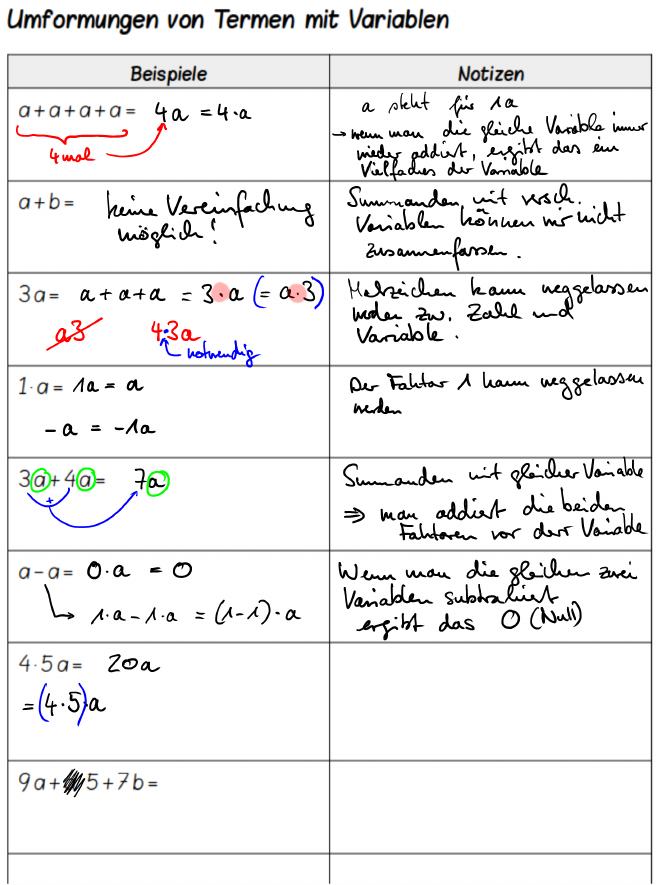
Ich bin recht zufrieden mit dem Ergebnis. Einer der wichtigsten Aspekte war immer die Betonung der Punkt-vor-Strich-Regel, die für kompliziertere Terme mit Variablen sehr wichtig ist.
Als Hausaufgabe sollten sie die Aktivität noch einmal durcharbeiten. Es wäre vielleicht besser gewesen, wenn ich andere Terme verwendet hätte, aber ich hatte nicht genug Zeit.
Die Schülerinnen und Schüler sollten die Aufgaben nun hoffentlich systematischer mit Hilfe der Regeln, die sie aufgeschrieben haben, bearbeiten können. Oberflächlich sah es zumindest so aus.
Übung ohne GraspableMath
In der folgenden Stunde erhielten die Schüler von mir ein Arbeitsblatt mit Aufgaben, d.h. Termen, die sie zunächst ohne GraspaleMath vereinfachen sollen. Ich gab noch Tipps, wie man nun, da man nicht einfach probieren kann, sich die Summanden markiert, um keinen Summand zu übersehen und vor allem auch um das Vorzeichen nicht zu vergessen.
Der QR-Code rechts unten führt auf ein GraspableMath-Whiteboard mit dem die Schüler überprüfen können, ob sie die Aufgaben richtig gelöst haben. Im Gegensatz zu den Aktivitäten mussten die Schüler hier noch ein paar neue Bedienfähigkeiten von GraspableMath anwenden, wie das Kopieren eine Ausdrucks, das Verschieben und das Löschen. Die meisten haben es aber gut hinbekommen.
Beim Herumgehen fiel mir auf, dass einige Schüĺer sich nicht an meine Hinweise zum Markieren der Summanden gehalten haben. Einige stellten mit Hilfe des GraspableMath-Whiteboards fest, dass sie einen Fehler haben und nahmen sich vor, die Summanden besser doch zu markieren.
Eine Schülerin war zu Beginn unsicher und ich schlug ihr vor, die erste Aufgabe doch einmal zuerst in dem Whiteboard durchzugehen, damit Sie noch einmal daran erinnert wird, was man zusammenfassen kann und was nicht.
Gut fand ich auch die Situation, als ein Schüler, der sonst eher schwächer war, den eher besseren Schüler belehrte, dass er die Punkt-vor-Strich-Regel beachten müsse. Das wurde dann in dem GraspableMath-Whiteboard kontrolliert und konnte korrigiert werden. Das motiviert sicherlich den ersten Schüler besonders.
Und? Was hat es gebracht?
Ob es langfristig etwas gebracht hat, kann ich noch nicht sagen. Aber mir hat gerade auch bei der Bearbeitung der Aufgaben auf dem letzten Arbeitsblatt gefallen, dass die Schüler das Whiteboard unterschiedlich einsetzen konnten. An verschiedenen Stellen der Bearbeitung. Und sie haben dabei GraspableMath, wie ich finde, sehr sinnvoll eingesetzt, wobei ich es Ihnen natürlich auch vorbereitet habe. Aber insgesamt eine gute Voraussetzung für später.
Insgesamt hatte ich zu wenig Aufgaben, denn einige waren am Ende etwas gelangweilt. Zum Teil auch, weil sie sich nicht an meinen Markierungs-Vorschlag gehalten haben. Ich habe sie dann beauftragt, das Arbeitsblatt am Beamer auszufüllen und es wurde von mir nur akzeptiert, wenn auch so markiert wurde, die ich es wollte. Dabei gab es das Zusammenspiel mit Schülern, die das Aufschreiben beobachteten und Fehler korrigierten. Insgesamt sicher sehr produktiv, leider wegen zu wenig Aufgaben für die Besseren etwas unruhig.

Ich bin also doch recht zufrieden mit dem Einsatz und ich glaube die Schüler fanden es auch nicht sooo schlecht. Zumindest nicht negativ 😉
Und weiter?
Uns fehlt zu den rationalen Zahlen noch die Multiplikation und die Division, ebenso die Potenzen. Nachdem wir das mit Zahlen behandelt haben, werden wir wieder zu Termen mit Variablen zurückkehren.
Ich bin noch nicht so ganz sicher, in welcher Reihenfolge es passieren wird, aber ich möchte noch einbauen:
- Einsetzen von Zahlen in Variablen – kann man auch in GraspableMath durchführen und bekommt dann ggf. auch Klammern ergänzt, wenn es nötig ist.
- Terme mit mehreren Zahlen-Faktoren – vor allem negative Faktoren verführen gerne dazu, die Punkt-vor-Strich-Rechnung zu ignorieren. Der typische Fehler beim Umformen von Termen.
- Potenzen von Variablen und wie man damit umgeht
Nicht als Thema werde ich an der Stelle und noch in diesem Schuljahr das Distributiv-Gesetz und die Minusklammern bearbeiten. Das kommt als Thema erst im nächsten Schuljahr vor. Diese Einführung hier, dient als Vorbereitung auf die Äquivalenzumformungen.

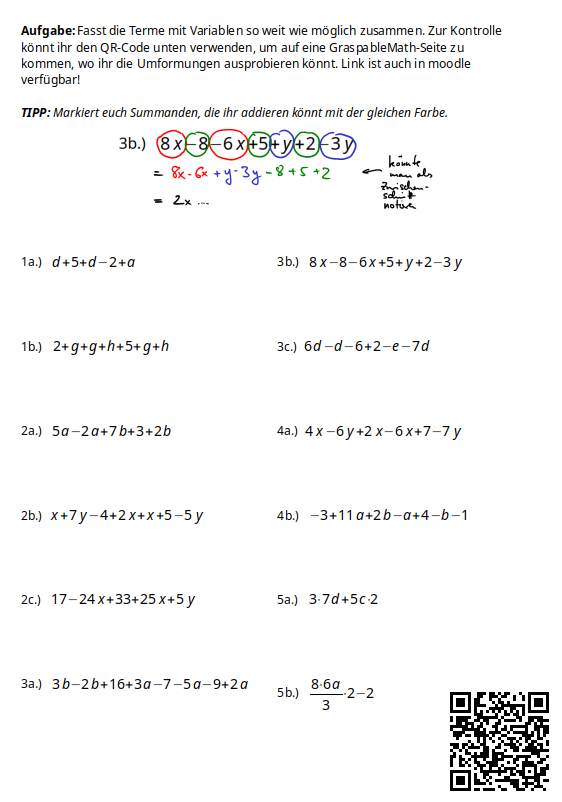
Antworten